I am curious if I could take lets say an 500mw 382nm laser diode and a lets say 910nm diode of the same power output density for a astigmatically corrected collimated beam/spot size and mix the 2 lasers and produce the difference frequency of 528nm or some other similar combination of various high power laser diodes at 382nm-920nm, I am used to doing this in audio work microwave uhf vhf. Can this be done by mixing of two lasers to produce the sum or difference frequencies???




 Reply With Quote
Reply With Quote


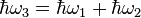 Ok so the energy of the 3rd produced sum wave has to equal the combined energy of the first 2 primary waves.
Ok so the energy of the 3rd produced sum wave has to equal the combined energy of the first 2 primary waves.
 . Here, the coefficients χ(n) are the n-th order
. Here, the coefficients χ(n) are the n-th order  , where c.c. denotes the
, where c.c. denotes the  , where the summation is over
, where the summation is over . The six combinations (nx,mx) correspond, respectively, to the second harmonic of E1, the second harmonic of E2, the optically rectified signals of E1 and E2, the difference frequency, and the sum frequency. A medium that is thus pumped by the fields E1 and E2 will radiate a field E3 with an angular frequency ω3 = m1ω1 + m2ω2.
. The six combinations (nx,mx) correspond, respectively, to the second harmonic of E1, the second harmonic of E2, the optically rectified signals of E1 and E2, the difference frequency, and the sum frequency. A medium that is thus pumped by the fields E1 and E2 will radiate a field E3 with an angular frequency ω3 = m1ω1 + m2ω2. , at position
, at position  , with the wave vector
, with the wave vector  , where c is the velocity of light and n(ωj) the index of refraction of the medium at angular frequency ωj. Thus, the second-order polarization angular frequency ω3 is
, where c is the velocity of light and n(ωj) the index of refraction of the medium at angular frequency ωj. Thus, the second-order polarization angular frequency ω3 is . At each position
. At each position  . Constructive interference, and therefore a high intensity ω3 field, will occur only if
. Constructive interference, and therefore a high intensity ω3 field, will occur only if . The above equation is known as the phase matching condition. Typically, three-wave mixing is done in a birefringent crystalline material (I.e., the
. The above equation is known as the phase matching condition. Typically, three-wave mixing is done in a birefringent crystalline material (I.e., the  )
)


 where Ej are the electric field amplitudes. Ξ1 and Ξ2 are known as the two pump waves, with Ξ3 being the signal wave, and Ξ4 being the generated conjugate wave.
where Ej are the electric field amplitudes. Ξ1 and Ξ2 are known as the two pump waves, with Ξ3 being the signal wave, and Ξ4 being the generated conjugate wave. . This is the generating field for the phase conjugate beam, Ξ4. Its direction is given by k4 = k1 + k2 - k3, and so if the two pump beams are counterpropagating (k1 = -k2), then the conjugate and signal beams propagate in opposite directions (k4 = -k3). This results in the retroreflecting property of the effect.
. This is the generating field for the phase conjugate beam, Ξ4. Its direction is given by k4 = k1 + k2 - k3, and so if the two pump beams are counterpropagating (k1 = -k2), then the conjugate and signal beams propagate in opposite directions (k4 = -k3). This results in the retroreflecting property of the effect. (where c is the speed of light). If the pump beams E1 and E2 are plane (counterpropagating) waves, then:
(where c is the speed of light). If the pump beams E1 and E2 are plane (counterpropagating) waves, then: ; that is, the generated beam amplitude is the complex conjugate of the signal beam amplitude. Since the imaginary part of the amplitude contains the phase of the beam, this results in the reversal of phase property of the effect.
; that is, the generated beam amplitude is the complex conjugate of the signal beam amplitude. Since the imaginary part of the amplitude contains the phase of the beam, this results in the reversal of phase property of the effect.

 Back to the Optical Frequency Combs
Back to the Optical Frequency Combs 
